1) Μια παίκτρια του golf που εξασκείται σε υπερυψωμένο επίπεδο κατά 5 m, κτυπάει τη μπάλα που φεύγει με οριζόντια ταχύτητα 20m/s. Υποθέτουμε g=10m/s2 .
α) πόσο χρόνο θα κάνει η μπάλα να κτυπήσει στο έδαφος;
β) Ποια είναι η οριζόντια απόσταση που θα διανύσει;
γ) Ποια είναι η επιτάχυνση της μπάλας 0,5 sec μετά που θα κτυπηθεί;
δ) Υπολογίστε την ταχύτητα της μπάλας 0,80 sec μετά το κτύπημα.
ε) Με ποια ταχύτητα θα κτυπήσει η μπάλα το έδαφος;
α.1sec β.20m γ.10 m/s2 δ. 21,5m/s ε.22,3m/s
2) Ένας οδηγός μηχανής σε ταινία πηδάει οριζόντια από την κορυφή λόφου ύψους 50m. Πόσο γρήγορα (σε km/h) πρέπει να φύγει από την κορυφή αν πρέπει να προσγειωθεί σε απόσταση 90m από τη βάση του λόφου;
g=9,8m/s2

Οριζόντια βολή συμβαίνει
όταν ένα αντικείμενο έχει ταυτόχρονα
κάθετη και οριζόντια κίνηση. Αυτό γίνεται
όταν ένα αντικείμενο εκτοξεύεται ίσια,
όχι με γωνία και πέφτει μέχρι να χτυπήσει
το έδαφος. Το κυριότερο που πρέπει να
θυμόμαστε όταν δουλεύουμε με οριζόντια
βολή, είναι ότι παρόλο που το αντικείμενο
έχει συγχρόνως οριζόντια και κάθετη
κίνηση, οι δύο συνιστώσες θα αντιμετωπιστούν
ξεχωριστά. Όταν κάτι εκτοξεύεται
οριζόντια από το ίδιο ύψος αλλά με
διαφορετική δύναμη, θα χρειαστεί πάντα
τον ίδιο χρόνο να φθάσει στο έδαφος.
Όσο
πιο μεγάλη η αρχική δύναμη, τόσο πιο
μακριά θα πάει το αντικείμενο, αλλά όλα
θα προσγειωθούν στον ίδιο χρόνο.
Η αιτία όπως είπαμε
πριν, είναι ότι η κάθετη κίνηση δεν
εξαρτάται (δεν επηρεάζεται δηλαδή) από
την οριζόντια. Ένα σώμα θα πέφτει πάντα
με επιτάχυνση 9.8 m/sec2.. Έτσι όπως
βλέπετε παίρνει πάντα το ιδιο ποσό
χρόνου να κτυπήσει στο έδαφος, η διαφορά
είναι μόνο πόσο μακριά θα προσγειωθεί
από το αρχικό σημείο που το εκτοξεύσαμε.
Έτσι το πρώτο πράγμα
που θα πρέπει να βρίσκουμε (ανάλογα
βέβαια και με τι μας ζητάνε) είναι να
βρούμε τον χρόνο που είναι στον αέρα. Άμα το βρούμε αυτό, όλα τα άλλα είναι εύκολα. Ένα παράδειγμα.
(Στα παρακάτω νούμερα οι τελείες στα νούμερα δείχνουν δεκαδικούς αριθμούς)
Ένα κανόνι ρίχνει οριζόντια μια βόμβα από ένα λόφο 24m ψηλό, που προσγειώνεται 100m, από τη βάση του.
α) Με ποιά ταχύτητα ρίχτηκε το βλήμα;
β) με ποιά ταχύτητα προσγειώνεται;
Στην οριζόντια βολή, αφού το βλήμα ρίχτηκε οριζόντια, η αρχική κάθετη ταχύτητα (μέτρο) είναι 0m/sec. Θα βρούμε το χρόνο πτήσης. Αφού ξέρουμε το ύψος του λόφου και την κάθετη επιτάχυνση θα χρησιμοποιήσουμε τον τύπο:
Έτσι θα έχουμε όπως παρακάτω:

Τώρα σύμφωνα με τον πρώτο νόμο του Νεύτωνα, ένα αντικείμενο ταξιδεύει με σταθερή ταχυτητα εκτός και αν ασκηθεί επάνω του εξωτερική δύναμη. Αφού δεν υπάρχει εξωτερική δύναμη πάνω στην οβίδα καθώς ταξιδεύει οριζόντια (αμελούμε την αντίσταση του αέρα), μπορούμε να δεχτούμε ότι κινείται με σταθερή ταχύτητα.
Σιγά! Τι γίνεται με τη βαρύτητα; Θυμηθείτε ότι η βαρύτητα επηρεάζει την κάθετη κίνηση και αφού κάθετη και οριζόντια είναι ξέχωρες οντότητες, δεν επηρεάζει την οριζόντια κίνηση της βόμβας. Έτσι είναι απλό να υπολογίσουμε την αρχική ταχύτητα της.

που είναι και η απάντηση στο πρώτο ερώτημα.
Για το δεύτερο ερώτημα, μπορούμε να βρούμε την κάθετη ταχύτητα αφού γνωρίζουμε την επιτάχυνση και τον χρόνο να πάει κάτω.(= χρόνο να διανύσει τα 100m)

Οκ, αυτό ήταν εύκολο. Για περιμένετε όμως! δεν τελειώσαμε ακόμα! Στην αρχη του προβλήματος η βόμβα είχε μόνο την οριζόντια ταχύτητα και τώρα έχει και τις δύο, έτσι πρέπει να τις προσθέσουμε. Πριν από λίγο υπολογίσαμε την κάθετη συνιστώσα και αφού η οριζόντια είναι σταθερή, με απλό υπολογισμό βρίσκουμε την τελική ταχύτητα πρόσκρουσης.
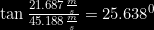
^{2}&space;+\left&space;(&space;21.687&space;\right&space;)^{2}\right&space;)}\frac{m}{s}=50.123\frac{m}{s})
Έτσι βρήκαμε τελικά ότι η ταχύτητα με την οποία κτυπάει κάτω είναι 50,123m/sec στι; 25,638 μοίρες με την οριζόντιο.
(Στα παρακάτω νούμερα οι τελείες στα νούμερα δείχνουν δεκαδικούς αριθμούς)
α) Με ποιά ταχύτητα ρίχτηκε το βλήμα;
β) με ποιά ταχύτητα προσγειώνεται;
Στην οριζόντια βολή, αφού το βλήμα ρίχτηκε οριζόντια, η αρχική κάθετη ταχύτητα (μέτρο) είναι 0m/sec. Θα βρούμε το χρόνο πτήσης. Αφού ξέρουμε το ύψος του λόφου και την κάθετη επιτάχυνση θα χρησιμοποιήσουμε τον τύπο:
Έτσι θα έχουμε όπως παρακάτω:
Τώρα σύμφωνα με τον πρώτο νόμο του Νεύτωνα, ένα αντικείμενο ταξιδεύει με σταθερή ταχυτητα εκτός και αν ασκηθεί επάνω του εξωτερική δύναμη. Αφού δεν υπάρχει εξωτερική δύναμη πάνω στην οβίδα καθώς ταξιδεύει οριζόντια (αμελούμε την αντίσταση του αέρα), μπορούμε να δεχτούμε ότι κινείται με σταθερή ταχύτητα.
Σιγά! Τι γίνεται με τη βαρύτητα; Θυμηθείτε ότι η βαρύτητα επηρεάζει την κάθετη κίνηση και αφού κάθετη και οριζόντια είναι ξέχωρες οντότητες, δεν επηρεάζει την οριζόντια κίνηση της βόμβας. Έτσι είναι απλό να υπολογίσουμε την αρχική ταχύτητα της.
που είναι και η απάντηση στο πρώτο ερώτημα.
Για το δεύτερο ερώτημα, μπορούμε να βρούμε την κάθετη ταχύτητα αφού γνωρίζουμε την επιτάχυνση και τον χρόνο να πάει κάτω.(= χρόνο να διανύσει τα 100m)
Οκ, αυτό ήταν εύκολο. Για περιμένετε όμως! δεν τελειώσαμε ακόμα! Στην αρχη του προβλήματος η βόμβα είχε μόνο την οριζόντια ταχύτητα και τώρα έχει και τις δύο, έτσι πρέπει να τις προσθέσουμε. Πριν από λίγο υπολογίσαμε την κάθετη συνιστώσα και αφού η οριζόντια είναι σταθερή, με απλό υπολογισμό βρίσκουμε την τελική ταχύτητα πρόσκρουσης.

